关系代数是一种抽象的查询语言，它用对关系的运算来表达查询。

关系代数的运算可以分别传统的集合运算和专门的关系运算两类。其中，传统的集合元素将关系看成元组的集合，其运算是从关系的“水平”方向，即行的角度来进行；而专门的关系运算不仅涉及行，更涉及列。

一、传统的集合运算

传统的集合运算是二目运算，包括并、差、交、笛卡儿积四种运算。

设关系 R 和关系 S 等目（具有相同的目 n，即两个关系都有 n 个属性）且同域（对应的属性都取自同一个域）。 t 是元组变量， t ∈ R 表示 t 是 R 的一个元组。

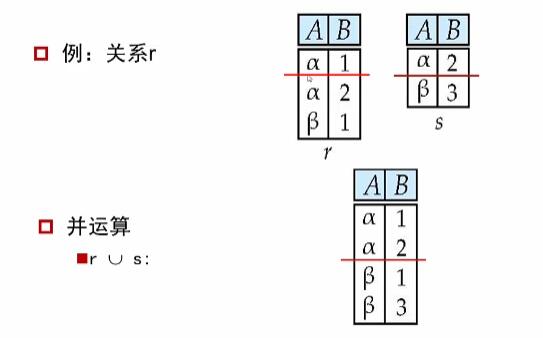
1.并

R ∪ S = {t | t ∈ R or t ∈ S}

由属于 R 或属于 S 的元组组成。

由于关系不允许重复元组，因此应该在“并”之后删除重复部分。

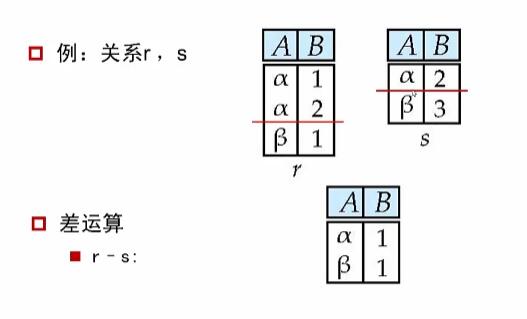
2.差

R - S = {t | t ∈ R and t ∉ S}

由属于 R 且不属于 S 的元组组成。

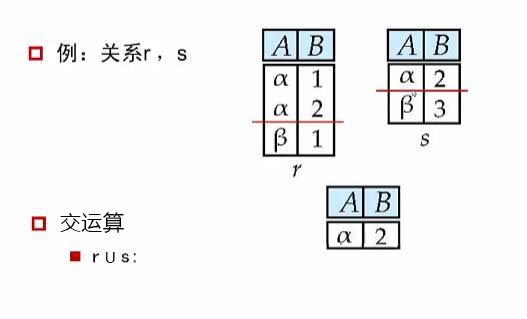
3.交

R ∩ S = {t | t ∈ R and t ∈ S}

由属于 R 又属于 S 的元组组成。

可以用差来表示， R ∩ S = R - (R - S) ， R 减去只属于 R 的部分，就可以得到 R 和 S 共有的部分。

4.笛卡儿积

R ✖ S = {{t q} | t ∈ R and q ∈ S}

R 的元组和 S 的元组可以组合成的所有序列。

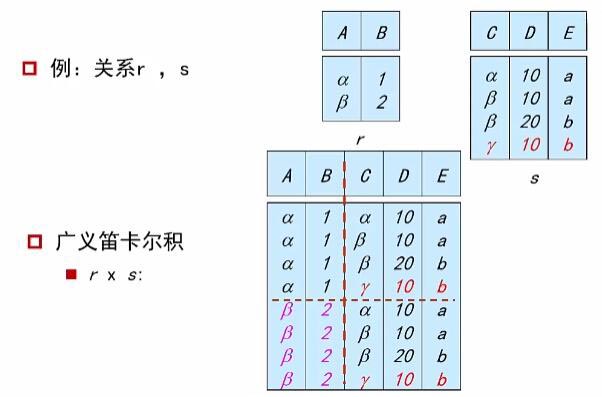
如果 R 和 S 的属性有交集，那么必须重命名这些有交集的属性。

二、专门的关系运算

专门的关系运算包括选择、投影、连接、除运算等。

设关系模式为 R(A₁, A₂, ···, A_n) ， R 为关系模式名， A₁, A₂, ···, A_n 为组成该关系的属性名的集合，它的一个关系设为 R 。 t 是元组变量， t ∈ R 表示 t 是 R 的一个元组。 t[A_i] 表示元组 t 中相对于属性 A_i 的一个分量。

1.选择

σₚ(R) = {t | t ∈ R and 条件}

在关系 R 中选择满足给定条件 P 的部分元组。

其中，

σ 代表选择；

P 表示选择条件，是针对元组中属性值的条件；

R 表示进行选择的关系；

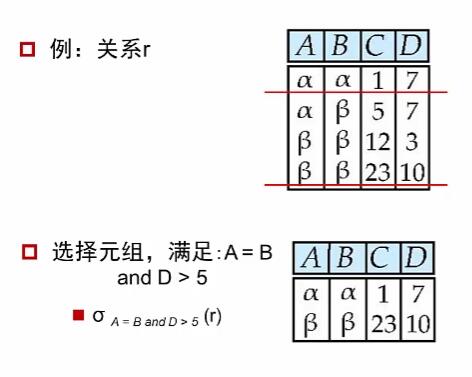
2.投影

Πᵪ(R) = {t[X] | t∈R}

在关系 R 中选择 X 中给出的若干属性，组成新的关系。

其中，

Π 代表投影；

X 为希望投影的属性列，运算结果中只会保留 X 中的属性；

R 表示进行投影的关系；

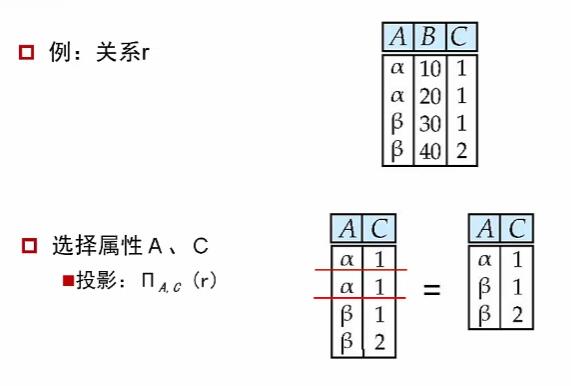
若进行投影后出现重复的元组，需要进行删除。

3.连接

(1) 连接

从两个关系的笛卡儿积中选择满足一定条件的元组。

其中，

▷◁ 代表连接；

A B 分别是 R 和 S 上两个可比较的属性组；

AθB 为判断条件；

R S 为参与连接的两个关系；

(2) 等值连接

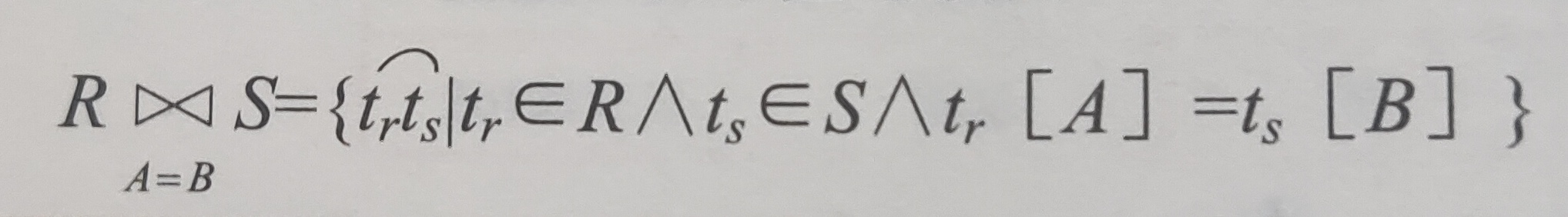
θ 为 = 的连接运算（A = B），即等值连接。从关系 R 和 S 的笛卡儿积中选取 A、B 属性值相等的元组。

例：

R = (A, B, C)，S = (D, E)

关系 R 和 S 关于 B 和 D 自然连接后的结果为：(A, B, C, D, E)

(3)自然连接

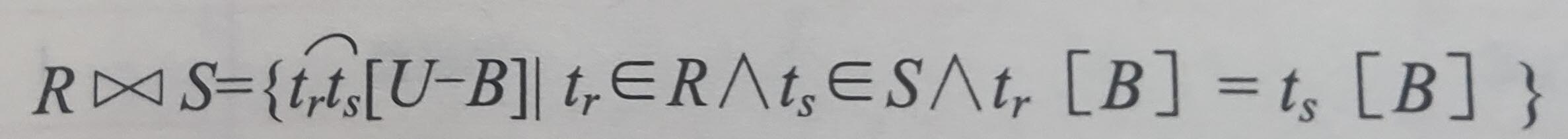
在自然连接的基础上再做一次投影，使相等的属性只保留一份。

例：

R = (A, B, C)，S = (B, D, E)

关系 R 和 S 关于 B 自然连接后的结果为：(A, B, C, D, E)

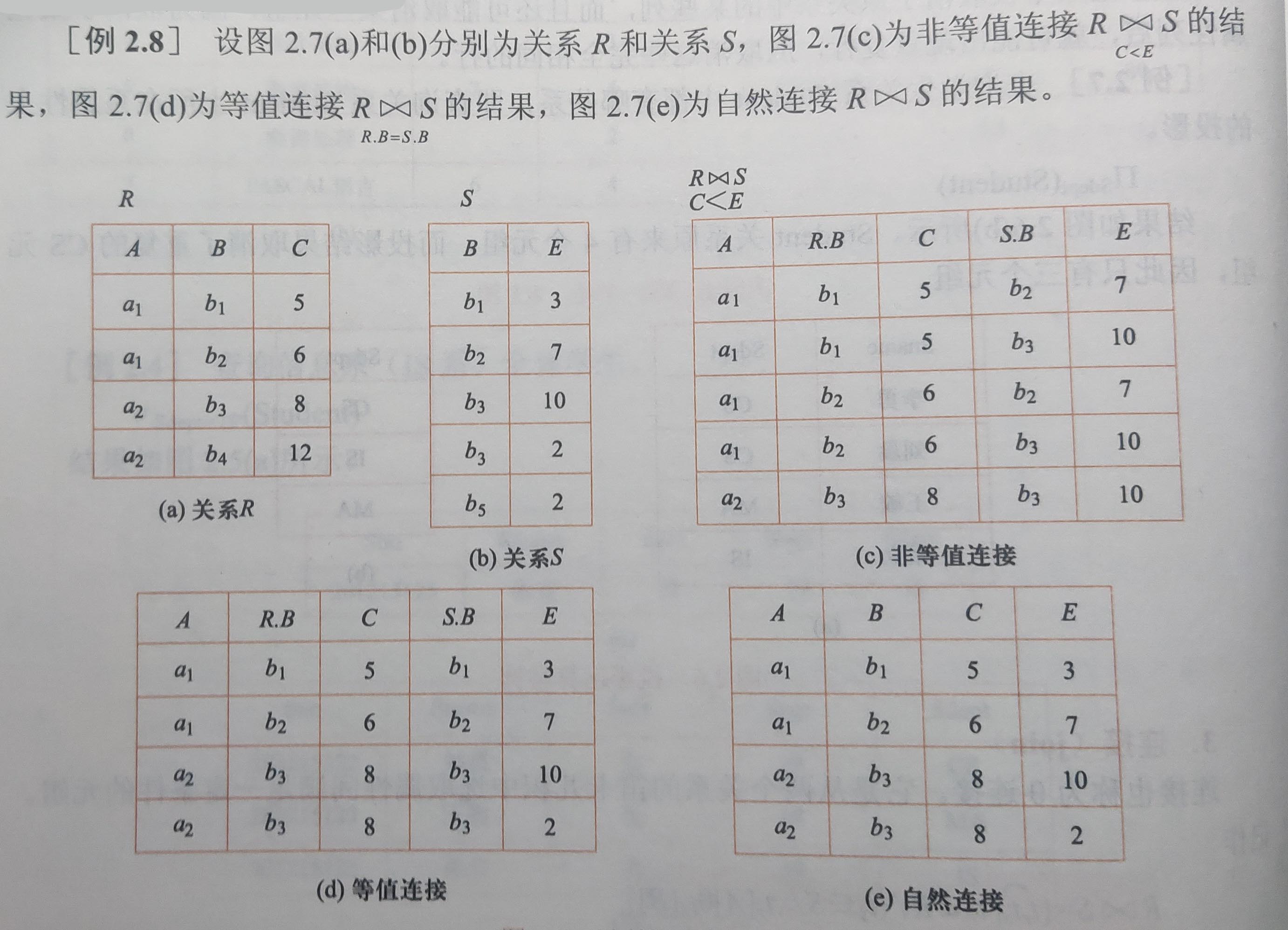
(4) 悬浮元组和外连接

在做自然连接时，某些元组没有两个关系上的公共属性，便会在操作时被舍弃，这些被舍弃的元组称为悬浮元组。

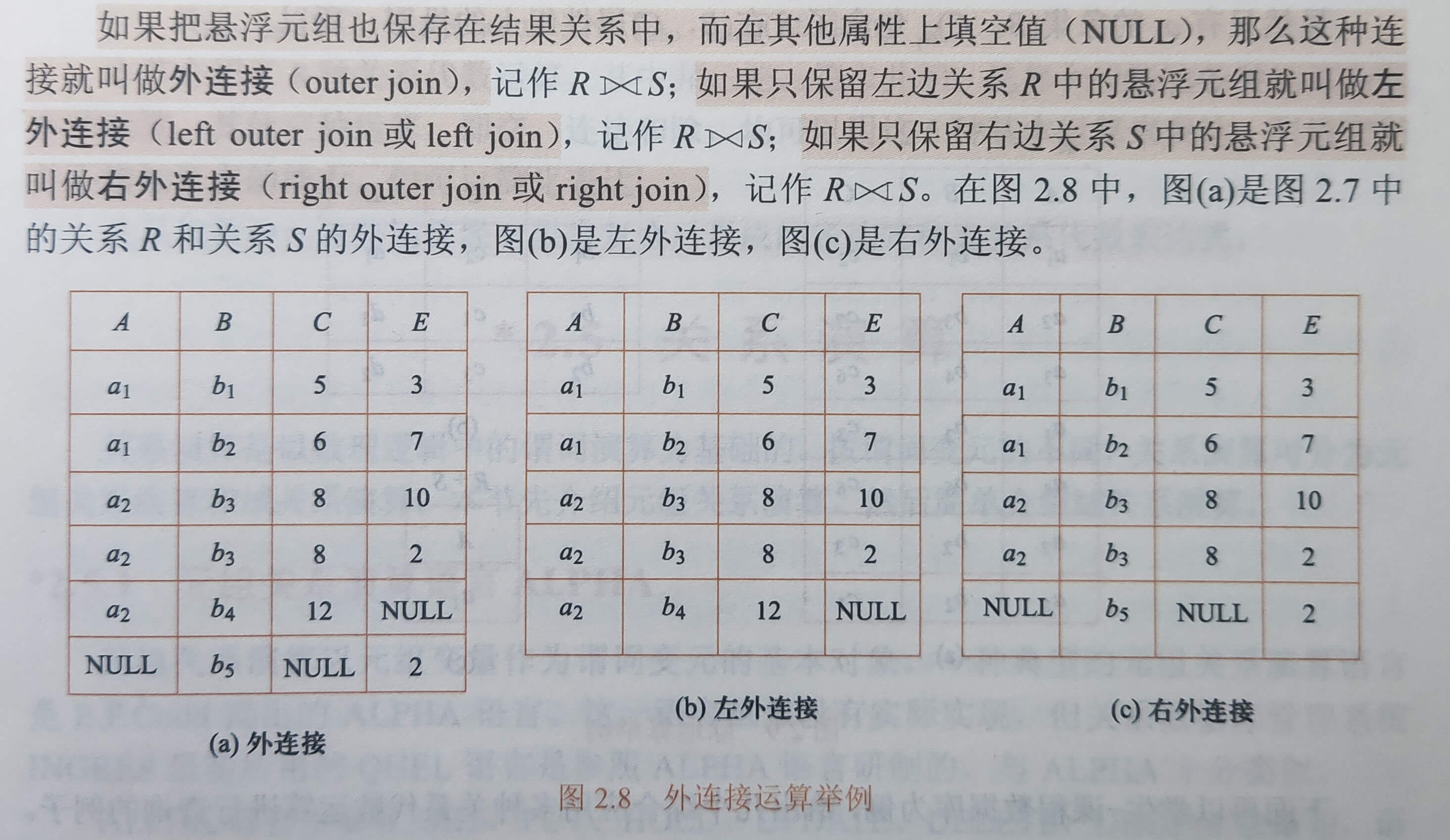
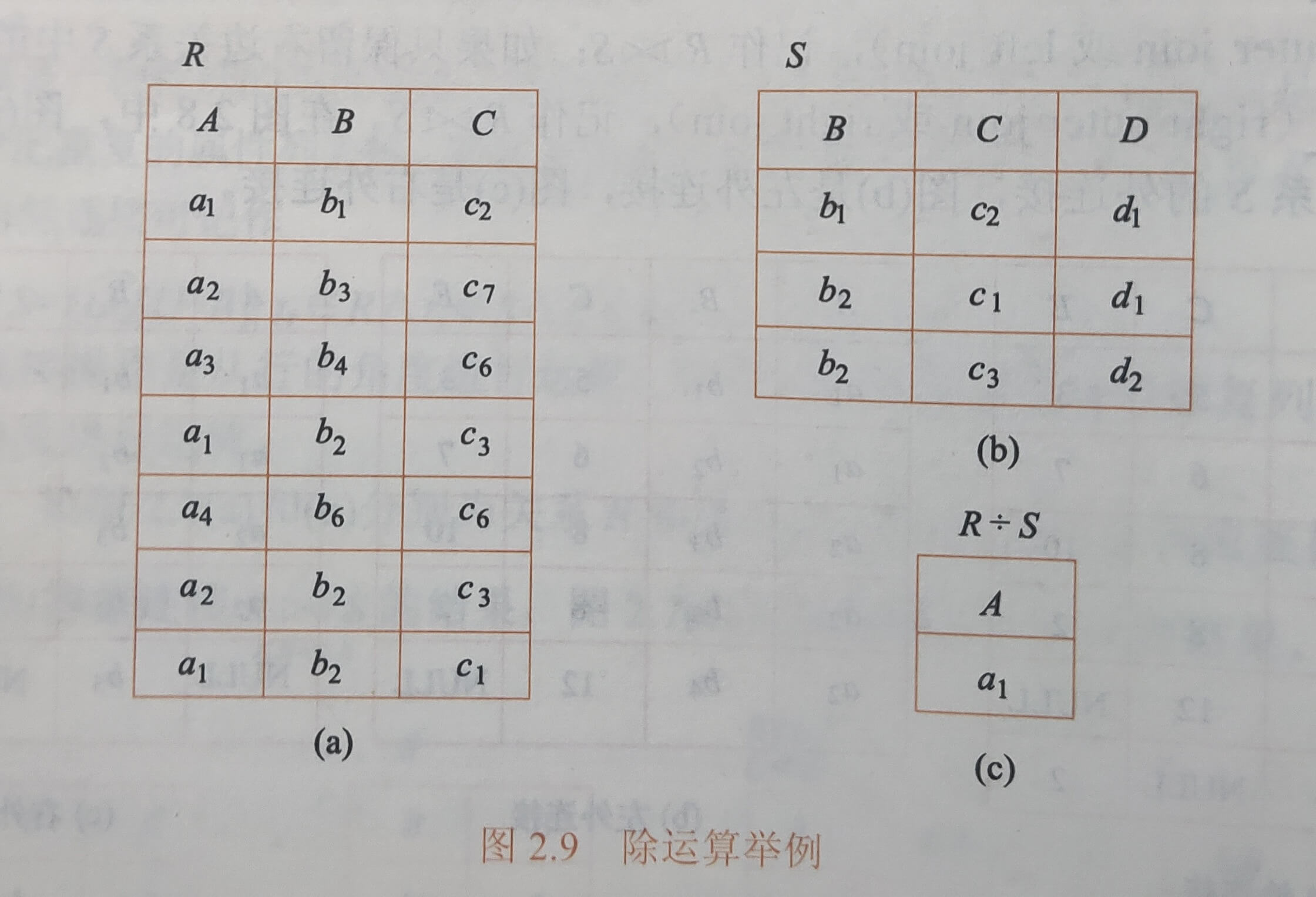
4.除

假设 R = (A, B, C, D) ，B = (C, D, E)

步骤：

• 对 R 做投影，只保留不存在于 S 中的属性，即保留 A, B
• 对 B 做投影，只保留存在于 R 中的属性，即保留 C, D
• 列出 R 中 A, B 取值的每一种可能时，对应元组中 C, D 的值的集合
• 若 A, B 的某种取值所对应元组中 C, D 的值的集合可以覆盖 B 投影中的所有值，则将其放入结果

三、其它关系运算

1.更名

ρᵪ(R)

将关系 R 改名为 X。

ρᵪ_{(A1, A2, ···, An)}(R)

将关系 R 改名为 X ，并将属性重命名为 A₁, A₂, ···, A_n 。

​

参考

• 数据库系统概论