算法笔记 动态规划

动态规划将一个复杂的问题分解成若干子问题，通过综合子问题的最优解来得到原问题的最优解。

动态规划会将每个求解过的子问题的解记录下来，这样当下一次碰到同样的子问题时，就可以直接使用之前记录的结果，而不是重复计算。注意：虽然动态规划采用这种方式来提高计算效率，但不能说这种做法就是动态规划的核心。

一、动态规划的递归写法

动态规划的递归写法又被称为记忆化搜索

1.斐波那契数列

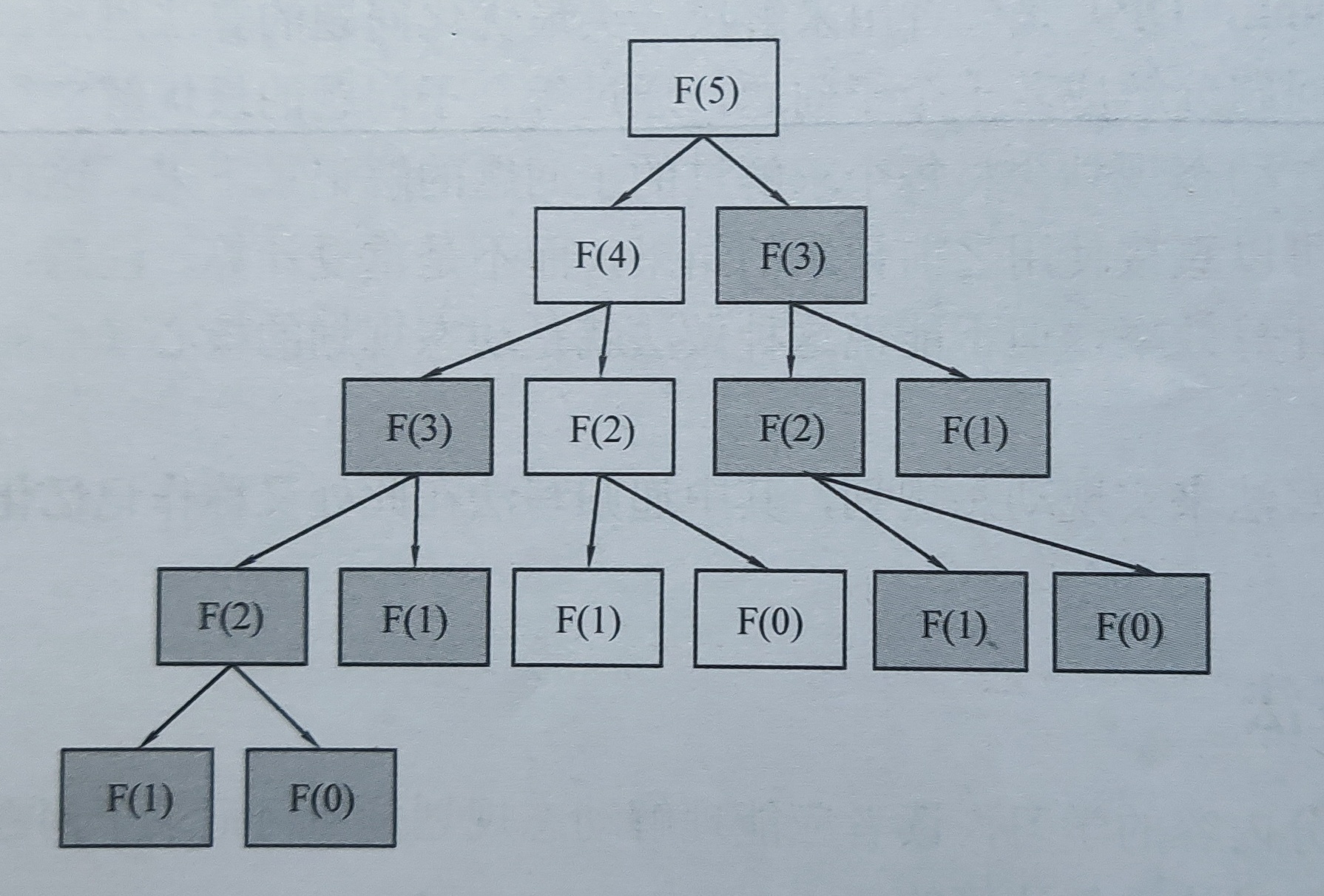
以斐波那契数列为例，其定义是： F0 = 1, F1 = 1, Fn = Fn-1 + Fn-2 ，之前的解题代码是这样：

1
2
3
4
int F(int n){
	if (n == 0 || n == 1)    return 1;
	else    return F(n - 1) + F(n - 2);
}

这样的递归写法会导致很多重复的运算，实际复杂度将高达 o(n2) 。

如图所示，在一次计算中，会有很大一部分数据被重复计算。当 n 的数量级很大时，重复计算的次数也将难以想象。

2.防止重复计算

为了避免重复计算，可以开一个一维数组，用以保存已经计算过的结果。在递归中判断结果是否已经计算，若计算过则直接取值，没计算过就计算后填入。

1
2
3
4
5
6
7
8
int F(int n){
	if (n ==0 || n == 1)    return 1;
	if (a[n] != -1)    return a[n];
	else{
		a[n] = f[n - 1] + f[n - 2];
		return a[n];
	}
}

通过记录已计算的内容，可以省去大半无效九三，这也是记忆化搜索这个名字的由来。通过记忆化搜索，仅多使用了 o(n) 的空间，就使时间复杂度从 o(n2) 降到 o(n) 。

二、动态规划的递推写法

数塔问题：将一些数字排成数塔的形状，其中第一层一个数字，第二层两个数字 ······ 第 n 层 n 个数字。现在要从第一层走到第 n 层，每次只能选择下一层连接的两个数字中的一个，求路径中数字的最大和是多少？

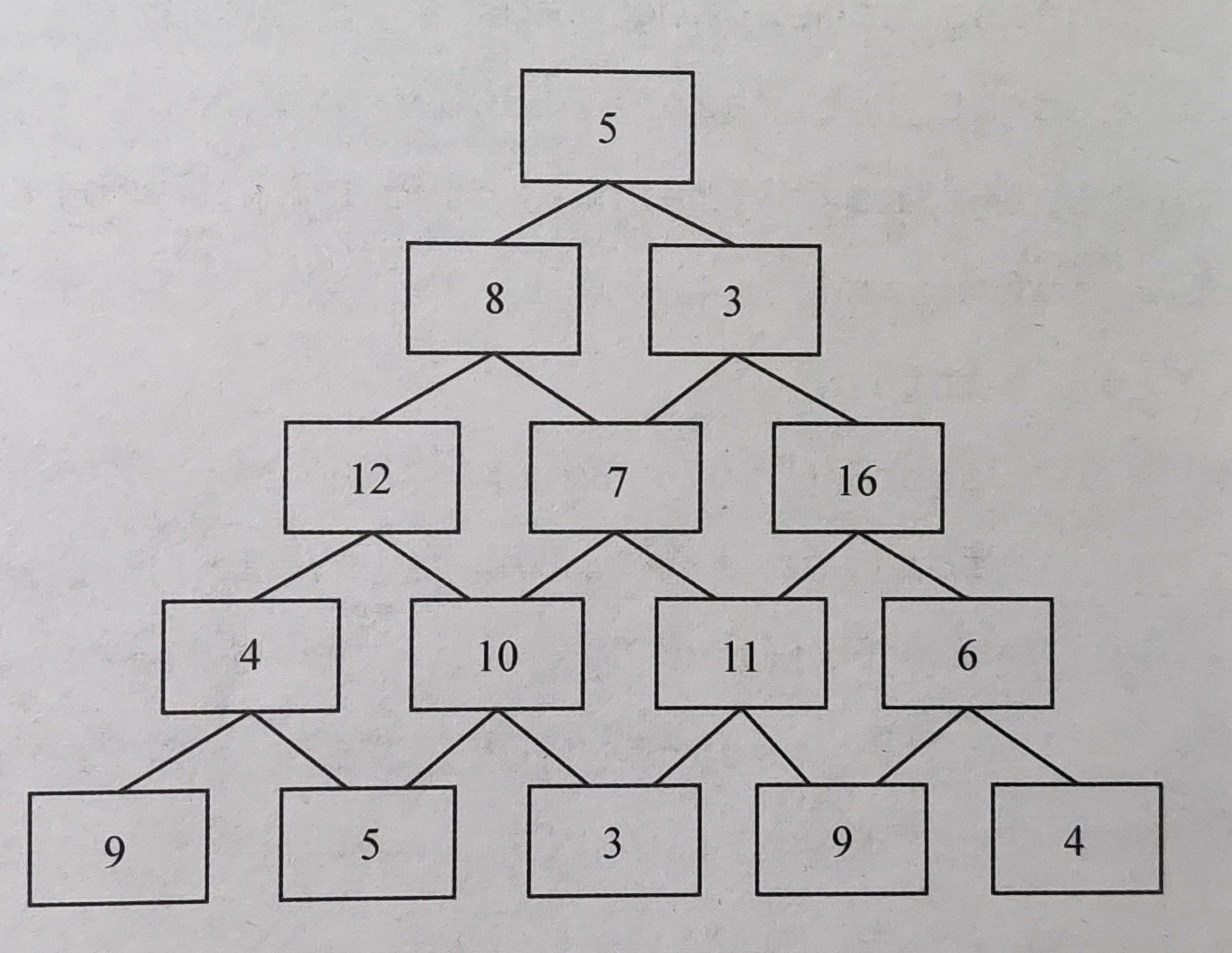
如果尝试穷举所有路径，时间复杂度将会是 o(2n) 。

还可以采用动态规划的递推写法解决问题。设 dp[i][j] 为第 i 行第 j 个数字到达底层的路径最大和，那么它就等于下面两个数字路径最大和的最大者，加上自身的数字，即 dp[i][j] = fmax(dp[i + 1][j], dp[i + 1][j + 1]) + f[i][j] 。动态规划的递推写法从边界出发，通过逐层向上递推得到最终的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <stdio.h>
#include <math.h>
const int maxn = 1000;
int f[maxn][maxn], dp[maxn][maxn];
int main(){
    int i, j;
    int n;
    scanf("%d", &n);
    for (i = 1; i <= n; i++){  //共有n列
        for (j = 1; j <= i; j++){  //每一列最多n个
            scanf("%d", &f[i][j]);
        }
    }
    for (i = 1; i <= n; i++){  //最底层的dp等于元素本身的值
        dp[n][i] = f[n][i];
    }
    for (i = n - 1; i >= 1; i--){  //从倒数第二层开始不断往上推
        for (j = 1; j <= i; j++){
            dp[i][j] = fmax(dp[i + 1][j], dp[i + 1][j + 1]) + f[i][j];
        }
    }
    printf("%d\n", dp[1][1]);
    return 0;
}

三、重叠子问题

如果一个问题可以被分解为若干个子问题，且这些子问题会重复出现，那么就称这个子问题拥有重叠子问题。

若此时使用一般的递归算法，将会导致程序一遍又一遍地计算相同的问题，因此可以用动态规划记录重叠子问题的解，来减少重复计算。一个问题必须拥有重叠子问题，才能使用动态规划解决。

四、最优子结构

如果一个问题的最优解可以由其子问题的最优解有效地构造出来，那么称这个问题拥有最优子结构。最优子结构保证了动态规划中原问题的最优解可以由子问题的最优解推导而来，因此，一个问题必须拥有最优子结构，才能使用动态规划去解决。

五、递推写法和递归写法

递推算法的思想是自底向上：从最简单的子问题开始，不断向上解决更大的问题，直至解决目标问题。

递归算法的思想是自顶向下：从目标问题开始，不断地将问题拆分为子问题，直至问题拆分得足够小，运算其结果后，再将结果逐层返回，直至算出目标问题的解。

六、分治和动态规划

  • 分治法和动态规划都是将问题分解为子问题，然后合并子问题的解得到原问题的解

  • 分治法分解出的子问题是不重叠的，因此分治法解决的问题不拥有重叠子问题

    动态规划解决的问题拥有重叠子问题

  • 分治法的子问题相互独立

    动态规划的子问题相互关联

  • 分治法解决的问题不一定是最优化问题

    动态规划解决的问题一定是最优化问题

七、贪心和动态规划

  • 贪心法和动态规划都要求原问题有最优子结构

  • 贪心法较为“短视”，对每一个子问题都选择最优解并抛弃掉其它选择，从而得到一个”全局的近似最优解”

    动态规划更加”长远“，不会放过任何一条路线，在最后选择最优解。

​

参考

  • 算法笔记