算法笔记 递归

本文将介绍递归这一常见的算法思想。

一、分治

分治，分而治之，将原问题划分为若干个规模较小而结构与原问题相同或相似的子问题，然后分别解决这些子问题，最后合并子问题的解，即可得到原问题的解。上面的定义体现出分治法的三大步骤：分解、解决、合并。

分治法分解出的子问题应该是相互独立、没有交叉的。

分治法作为一种算法思想，既可以使用递归的手段实现，也可以使用非递归的方法实现。一般来说，用递归实现较为容易。

二、递归

1.什么是递归

要理解递归，你要先理解递归，直到你能理解递归。

递归思想在于通过反复调用自身函数，使问题逐步缩小，直至缩小到可以轻松解决，再逐层返回最终求出原问题的解。

一个小例子：

士兵如果想知道自己在队列中的位置，一般有两个方法：

① 从头开始遍历整个队列，直到自己的位置为止。

② 递：依次向前传递口令“报数”，直至队列开头位置。

​ 归：队列开头的士兵报出自己的位置，之后的士兵依次根据前一名士兵的位置报出自己的位置。

1
2
3
4
5
6
int SoldierCount(士兵){
	if (队列未到开头){
		return 1 + f(前一个士兵);
	}
	else return 1;
}

2.重要概念

递归有两个重要概念：递归边界和递归式。

(1) 递归边界

是问题分解的尽头。递归应该是有限的，可终止的。

(2) 递归式

递归式是将原问题分解为若干子问题的手段。

3.求 n 的阶乘

n 的阶乘的计算式：

1
n! = 1 * 2 * ··· * n

n 的阶乘的递推形式：

1
n! = (n - 1)! * n

递归式：

1
F(n) = F(n - 1) * n

递归边界：

1
F(0) = 1

实现代码如下：

1
2
3
4
int fun(int n){
	if (n == 0)  return 1;
	else return fun(n - 1) * n;
}

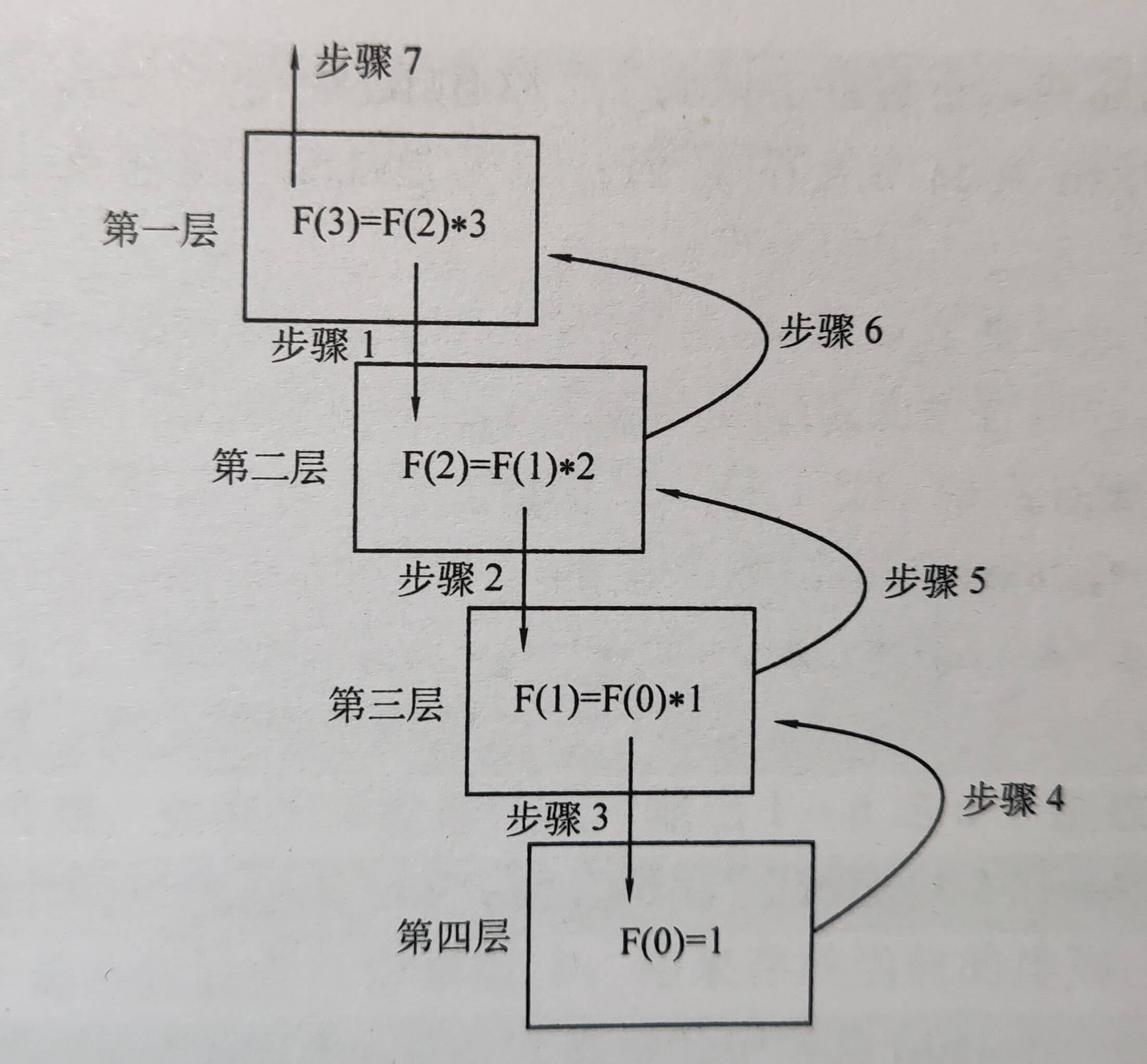
4.求 Fibonacci 数列的第 n 项

Fibonacci 数列（即斐波那契数列）是满足 F(0) = 1，F(1) = 1，F(n) = F(n - 1) + F(n - 2) 的数列，数列的前几项为 1，1，2，5，8，··· 。

递归式：

1
F(n) = F(n - 1) + F(n - 2)

递归边界：

1
2
F(0) = 1
F(1) = 1

实现代码如下：

1
2
3
4
int fun(int n){
	if (n == 0 || n == 1)  return 1;
	else return fun(n - 1) + fun(n - 2);
}

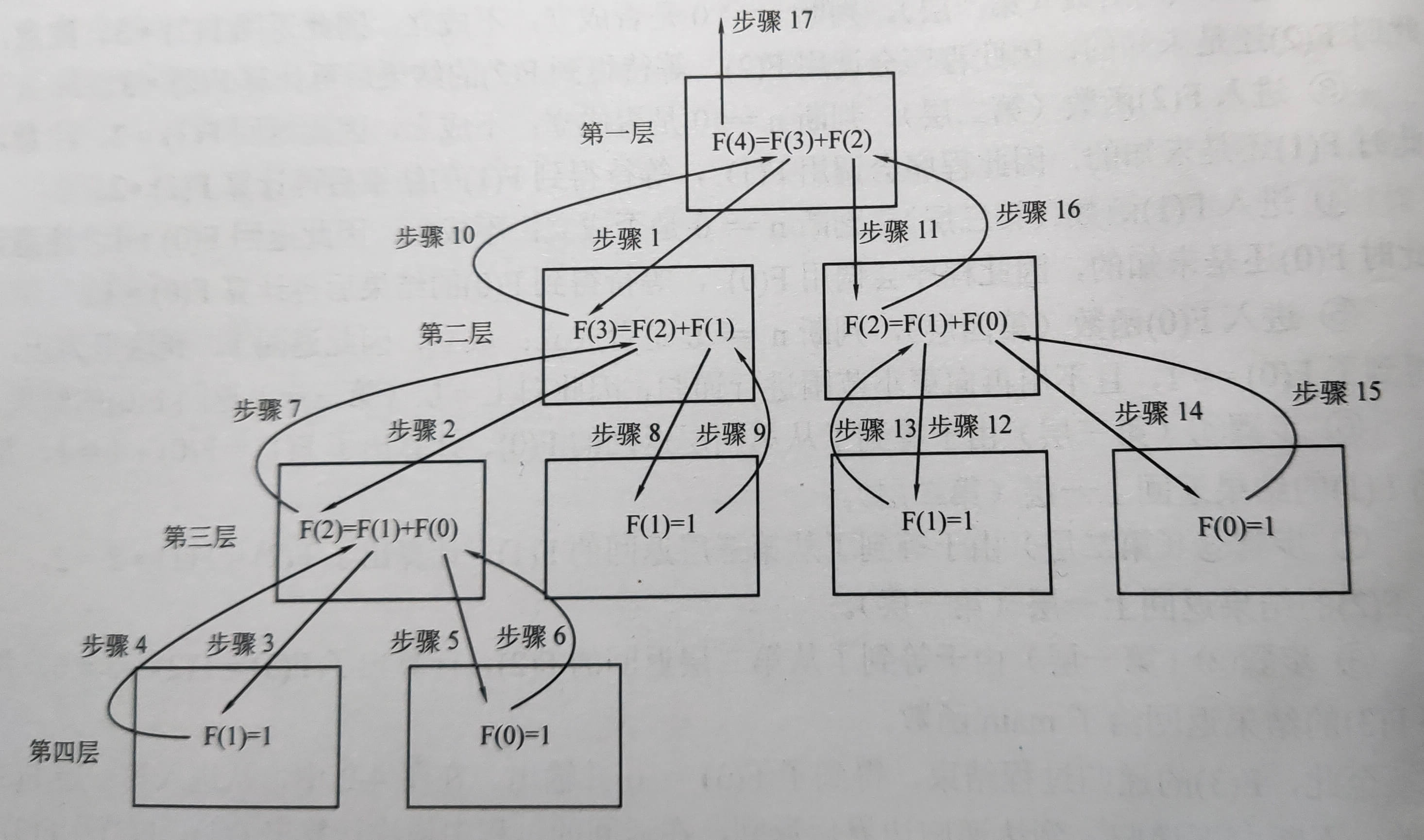
5.全排列

一般把 1 ~ n 这 n 个整数按某个顺序摆放的结果称为这 n 个整数的一个排列，而全排列指这 n 个整数能形成的所有排列。

例如 1、2、3 这三个整数，(123)、(132)、(213)、(231)、(312)、(321) 就是它们的全排列

现要求按字典序顺序输出 1~n 的全排列。

思路：

  • 按顺序枚举每一个位置可能出现的数字
  • 之前已经出现的数字不能再出现

设定一个数组 P ，用来存放当前的排列；再设定一个散列数组 hashTable ，其中 hashTable[x] 为 true 时表示整数已经在数组 P 中出现。按顺序往 P 中填入数字，不妨假设当前已经填好了 P[1] ~ P[index - 1] ，需要在 P[index] 中填入数字。此时从 1~n 依次枚举，若数字还未使用过，便填入，并将 hashTable[x] 设为 true ，继续处理 P[index + 1] 。当递归完成后，再将 hashTable[x] 还原为 false，以便填入下一个数字。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <stdio.h>

const int maxn = 11;
int n;
int P[maxn];  //排列
int hashTable[maxn] = {0};  //用于记录数字是否出现
void generateP(int index){
	if (index == n + 1){  //到达边界，说明此轮排列已经处理完成
		for (int i = 1; i <= n; i++){
            printf("%d", P[i]);
        }
		printf("\n");
	}
	else {
		// 若到达此处，说明排列未处理完
		for (int x = 1; x <= n; x++){  //从1开始枚举数字
			if(hashTable[x] == 0){
				P[index] = x;
				hashTable[x] = 1;
				generateP(index + 1);  //递归填下下一个空格，(0~index已确定后的)所有可能都会在此展开并完成
            	hashTable[x] = 0;  //将此数字标为未使用，继续在下一轮循环中尝试其它数字
			}
		}
	}
	
}
int main(){
	n = 3;
	generateP(1);
	return 0;
}

6. n 皇后

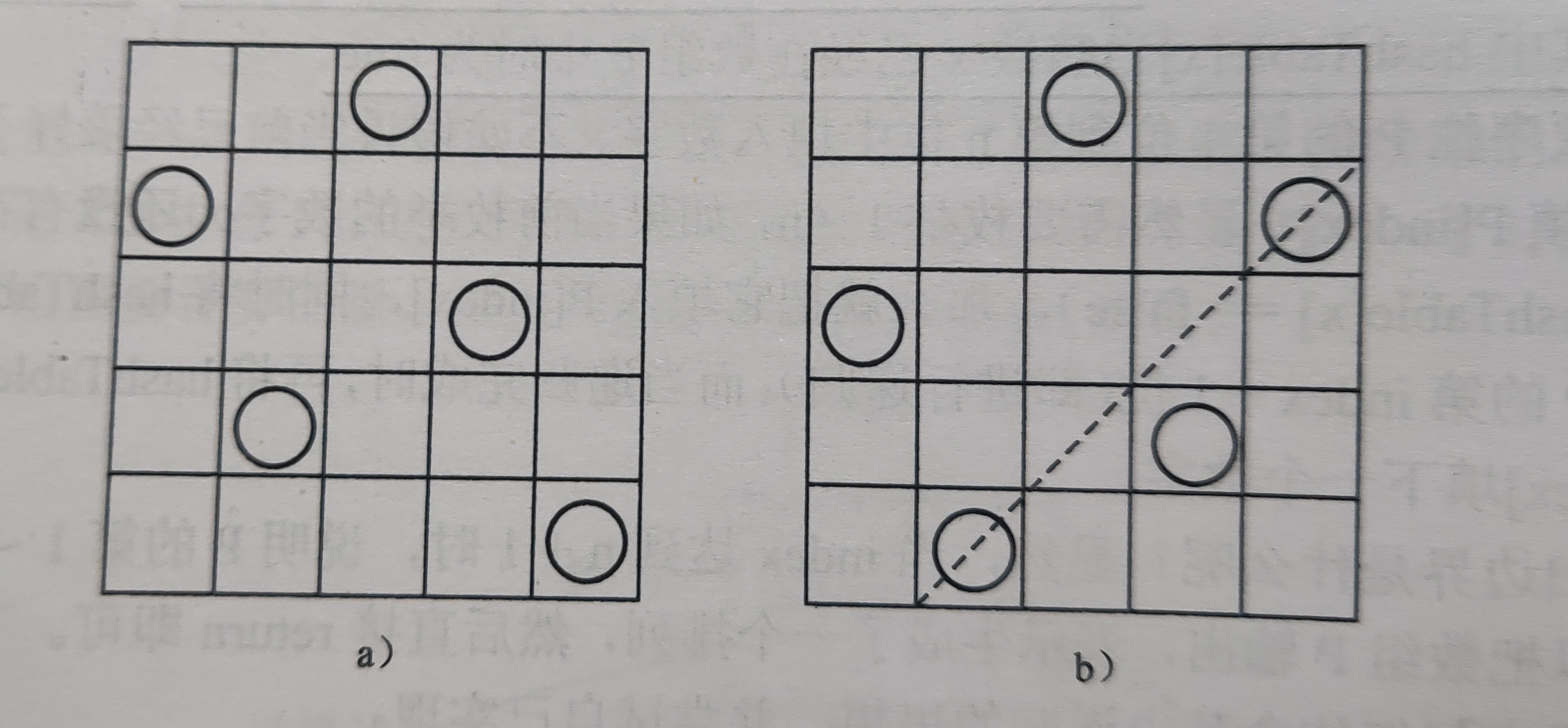
n 皇后问题是指在一个 n*n 的国际象棋棋盘上放置了 n 个皇后，得使这 n 个皇后两两均不在同一行、同一列、同一条对角线上（45 度线），求合法的方案数。

例如在 n = 5 的情况下，左图是合法方案，而右图是非法方案。

20210310001

方案一：

从 n2 个位置中选择 n 个位置，枚举每一种情况。这种方法需要极大的枚举量，如果 n 比较大，将会无法承受。

方案二：

因为皇后不能同行同列，因此可以参考全排列的方式解题。在每一列上尝试皇后放在各行上的可能，并标记为已使用，递归继续放置下一列。当枚举出每一种可能后，判断是否处于同一对角线，合法便计数，非法则抛弃。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include <stdlib.h>
int count = 0;
const int maxn = 11;
int n;
int P[maxn];  //排列
int hashTable[maxn] = {0};  //用于记录数字是否出现

void generateP(int index){
    if (index == n + 1){
        bool flag = true;
        for (int i = 1; i <= n; i++){
            for (int j = i + 1; j <= n; j++){
                if (abs(i - j) == abs(P[i] - P[j]))    
                    flag = false;  //在对角线上，不合法
            }
        }
        if (flag == true)  count++;  //合法时，计数器自增
        return;
    }
    /* 和全排列类似，依次枚举出每一列中元素可以在的行数。
       若元素被启用，则在对应数组上做出标记，递归放置下一列；
       此种情况的递归结束后，将对应数组标记取消，继续尝试下一种可能。
    */
    for (int x = 1; x <= n; x++){
        if (hashTable[x] == 0){
            P[index] = x;
            hashTable[x] = 1;
            generateP(index + 1);
            hashTable[x] = 0;
        }
    }
}

int main(){
	n = 8;
    printf("%d\n", count);
	generateP(1);
    printf("%d\n", count);
	return 0;
}

方案三：

可以对上述代码进行优化。当已经放置的皇后非法后，剩余皇后再怎么放置都会非法，因此便没有必要往下递归，直接返回上层即可。

一般来说，如果在到达递归边界前的某层，由于一些事实导致已经不再需要向下递归，可以直接返回上一层，这种方法一般称为回溯法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include <stdlib.h>
int count = 0;
const int maxn = 11;
int n;
int P[maxn];  //排列
int hashTable[maxn] = {0};  //用于记录数字是否出现

void generateP(int index){
    if (index == n + 1){  //到达此处说明一定合法（否则前面就已经被抛弃了）
        count++;
    }
    else{
        for (int x = 1; x <= n; x++){  //尝试此列的各种可能
            if (hashTable[x] == 0){  //若x行未被占用
                bool flag = true;  //先假设不会冲突
                for (int pre = 1; pre < index; pre++){  //遍历之前的皇后，判断此次的加入是否会造成非法
                    if (abs(index - pre) == abs(x - P[pre])){
                        flag = false;
                        break;  //冲突，推出此轮循环，继续尝试下一种可能
                    }
                }
                //不冲突，则此轮放置位置可用，向下递归。递归完成后，回复状态，继续下一轮玄幻，判断此轮的其它放置位置
                if (flag){   
                    P[index] = x;
                    hashTable[x] = 1;
                    generateP(index + 1);
                    hashTable[x] = 0;
                }
            }
        }
    }
}

int main(){
    n = 10;
    printf("%d\n", count);
	generateP(1);
    printf("%d\n", count);
	return 0;
}

7.汉诺塔

汉诺塔问题是这样的：三个座 A, B, C。开始时 A 中有 64 个盘子，盘子大小不等，大的在下，小的在上。要将这 64 个盘子从 A 座移到 C 座，但规定每次只允许移动一个盘，且在移动过程中 3 个座都必须保持大盘在下，小盘在上。移动过程中可以利用 B 座。要求编程序输出移动盘子的步骤。

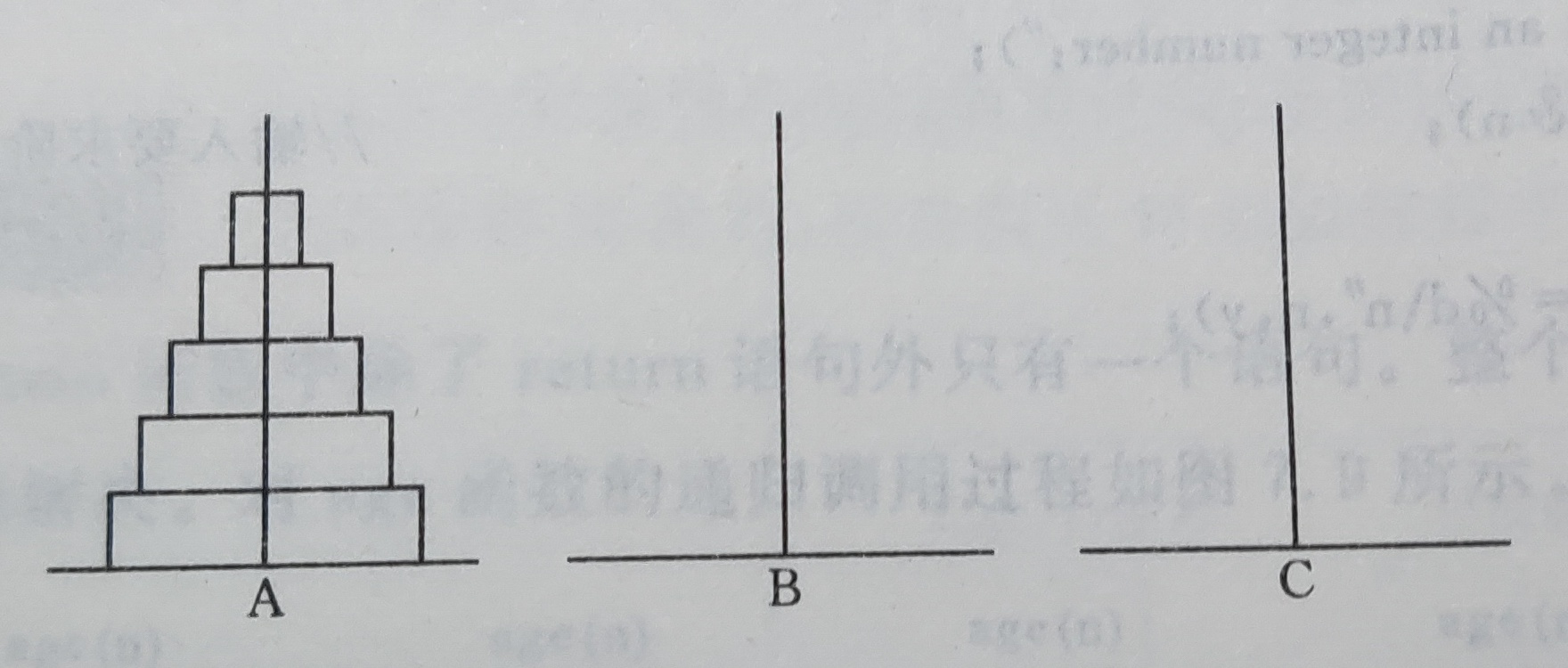
解题思路：

如何理解汉诺塔的递归？ - 知乎

第一个问题可以分为三步：

  • 将 63 个盘子从 A 移动到 B
  • 将最大的盘子从 A 移动到 C
  • 将 63 个盘子从 B 移到 C

而对于移动 63 个盘的问题，又可以再拆做三步，“层层下放”。

由上面分析可知，将 n 个盘子从 A 座移到 C 座可以分解为以下 3 个步骤：

  • 将 A 座上的 n - 1 个盘借助 C 座先移到 B 座。
  • 将 A 座上剩下的一个盘移到 C 座。
  • 将 n - 1 个盘从 B 座借助 A 座移到 C 座

由于第 n 个盘子一定大于 n - 1 个盘子，因此在移动 n - 1 个盘子时可以不用考虑底下的盘子。移动较小的盘子和在三个空塔里移动相同数量盘子的步骤应该相同，且必须相同。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <stdio.h>

void hanoi(int n, char one, char two, char three);
void move(char x, char y);

int main(){
    int m;
    printf("请输入盘子个数：");
    scanf("%d", &m);
    printf("移动%d个盘子的步骤是：\n", m);
    hanoi(m, 'A', 'B', 'C');
}

void hanoi(int n, char one, char two, char three){
    if (n == 1)  move(one, three);
    else{
        hanoi(n - 1, one, three, two);
        move(one, three);
        hanoi(n - 1, two, one, three);
    }
}

void move(char x, char y){
    printf("%c移至%c\n", x, y);
}

​

参考

  • 算法笔记