算法笔记二分法

本文将介绍二分法这一重要思想。

一、二分查找

1.猜数字

玩家 A 从一个范围中选择一个数，然后 B 玩家猜这个数字。

对于 B 玩家而言，每次从范围的中间数猜测是最好的办法。

2.线性查找

如何在一个严格递增序列中找出想要的数字？

一个显而易见的方法是：线性扫描整个序列，若扫描到则返回，扫描完都没有发现则查找失败。这种方法的时间复杂度是 o(n) 。

3.二分查找

二分查找必须基于有序序列

假设在序列 A 中查找元素 x ，

设 left = 0, right = length - 1 ；[left, right] 为查找区间
设 mid = (left + right) / 2

更好写法：mid = (left - right) / 2 + right
将 A[mid] 与 x 相比较，
- 若 A[mid] == x ，查找成功；
- 若 A[mid] > x ，设 right = mid - 1 ，继续查找；
- 若 A[mid] < x ，设 left = mid + 1 ，继续查找；
若 left > right ，查询失败。

二分查找的高效之处在于，每一步都可以去除当前区间中的一半元素，因此时间复杂度为 o(logn) 。

int Bsearch(int R[], int low, int high, int key){
	int mid;
	while (low <= high){
		mid = (low - high) / 2 + high;
		if (R[mid] == key)    return mid;
		else if (R[mid] > key)    high = mid - 1;
		else    low = mid + 1;
	}
	return -1;
}

3.查询元素区间

假设递增序列 A 中的元素可能重复，求序列中第一个大于等于 x 的元素的位置 L 以及第一个大于 x 的元素的位置 R 。

例如：

递增序列 {1, 3, 3, 3, 6}

查询 3 ，得 L = 1 ，R = 4 ；

查询 5 ，得 L = 4 ，R = 4 ;

查询 6 ，得 L = 4 ，R = 5 ；

查询 8 ，得 L = 5 ，R = 5 ;

(1) 分析：

当序列中有 x 时， L 应该指向第一个 x ， R 应该指向最后一个 x 的后一位；

当序列中没有 x 时， L 和 R 都应该指向第一个大于 x 的元素位置（插入 x 时 x 应在的位置）。

(2) 求 L ：

设 left = 0, right = length ；[left, right] 为查找区间

若 x 比所有元素都大，则应该指向序列的末尾的后一位
设 mid = (left + right) / 2
将 A[mid] 与 x 相比较，
- 若 A[mid] >= x ，说明 L 一定在 mid 左侧或 mid 处，应该往左子区间查询，并且不能抛弃 mid ，令 right = mid ；
- 若 A[mid] < x ，说明 L 一定在 mid 右侧，应该往右子区间查询，并且抛弃 mid ，令 left = mid + 1 ；
若 left == right ，查询成功，返回 left 或 right 。

1.当范围缩小至相差一格时，例如 left = 2，right = 3，则 mid = 2 ，若 A[mid] >= x ，则 right == mid == left ；若 A[mid] < x ，则 left == mid + 1 == left 。

2.当范围缩小至相差两格时，例如 left = 2，right = 4，则 mid = 3 ，若 A[mid] >= x ，则 right == mid ，变成相差一格的情况；若 A[mid] < x ，则 left == mid + 1 == left 。

因此，这种收缩方法一定可以使范围缩小至 left == right 。

查找的目标是找到一个位置，而不用判断此位置上的元素是否正确。因此，无需像二分查找一样当 left == right 时还要继续做判断，直接返回值就可以了。

代码如下：

int lowerbound(int A[], in left, int right, int x){
	int mid;
	while(left < right){
		mid = (left - right) / 2 + right;
		if (A[mid] >= x)    right = mid;
		else    left = mid + 1;
	}
	return left;
}

(3) 求 R：

设 left = 0, right = length ；[left, right] 为查找区间

若 x 比所有元素都大，则应该指向序列的末尾的后一位
设 mid = (left + right) / 2
将 A[mid] 与 x 相比较，
- 若 A[mid] > x ，说明 L 一定在 mid 左侧或 mid 处，应该往左子区间查询，并且不能抛弃 mid ，令 right = mid ；
- 若 A[mid] <= x ，说明 L 一定在 mid 右侧，应该往右子区间查询，并且抛弃 mid ，令 left = mid + 1 ；
若 left == right ，查询成功，返回 left 或 right 。

相比求 L 的代码，修改的是比较时的判断语句（ A[mid] > x 和 A[mid] <= x ）

代码如下：

int upperbound(int A[], in left, int right, int x){
	int mid;
	while(left < right){
		mid = (left - right) / 2 + right;
		if (A[mid] > x)    right = mid;
		else    left = mid + 1;
	}
	return left;
}

4.解题模板

用于解决“寻找有序序列第一个满足某条件的元素的位置”问题的固定模板

left = 0，right = length

int fun(int left, int right){
	int mid;
	while (left < right){
		mid = (left - right) / 2 + right;
		if (条件)    right = mid;
		else    left = mid + 1;
	}
	return left;
}

用于解决“寻找有序序列第一个不满足某条件的元素的位置”问题的固定模板

left = 0，right = length

int fun(int left, int right){
	int mid;
	while (left < right){
		mid = (left - right) / 2 + right;
		if (条件)    right = mid;
		else    left = mid + 1;
	}
	return left - 1;
}

二、二分法扩展

1.根号

如何计算“根号二”的近似值。

令 left = 1 right = 2
令 mid = (left + right) / 2
将 mid² 与 2 相比较，
- 若 mid * mid > 2 ，应在左区间中继续查找，令 right = mid
- 若 mid * mid < 2 ，应在右区间中继续查找，令 left = mid
- 若 right - left <= eqs ，查找成功，结束循环

解题代码：

const double eps = 1e-5;  //精度要求
double fun(double x){
	return x * x;
}
double calSqrt(){
	double left, right, mid;
	left = 1;
	right = 2;
	while (right - left > eqs){
		mid = (left + right) / 2;
		if (fun(mid) > 2)    right = mid;
		else   left = mid;
	}
	return mid;
}

2.求根问题

计算“根号二”的近似值实际上是这样一个问题的特例：给定一个区间，给定一个函数 f(x) ，求方程 f(x) = 0 的根 。

解题代码：

const double eqs = 1e-5;
double fun(double x){  //根据函数的不同而不同
	···
}
double solve(double L, double R){
	double mid;
	while (L - R > eqs){
		mid = (L + R) / 2;
		if (fun(mid) > 0)    right = mid;
		else    left = mid;
	}
	return mid;
}

3.一些错误

上文中的 1.根号 和 2.求根问题 都是摘抄原书代码，但个人觉得解题逻辑有些问题，解释如下：

函数的终止条件不应该是两个差值小于精度要求，而应该是 mid 的函数值小于要求
在判断条件中，若 f(mid) == 0 ，应该直接返回值，而不是继续划分区间

修改后代码如下：

const double eqs = 1e-5;
double fun(double x){  //根据函数的不同而不同
	···
}
double solve(double L, double R){
	double mid;
	mid = (L + R) / 2;
	while (fabs(fun(mid) - 2) > eqs){
		mid = (L + R) / 2;
		if (fun(mid) > 0)    right = mid;
		else if (fun(mid) < 0)   left = mid;
		else break;
	}
	return mid;
}

4.装水问题

要求在半径为 R 的半圆容器中注入水，水的高度为 h ，使得有水的面积 S1 与半圆面积 S2 的比例正好为 r 。给定 R 和 r ，求高度 h 。

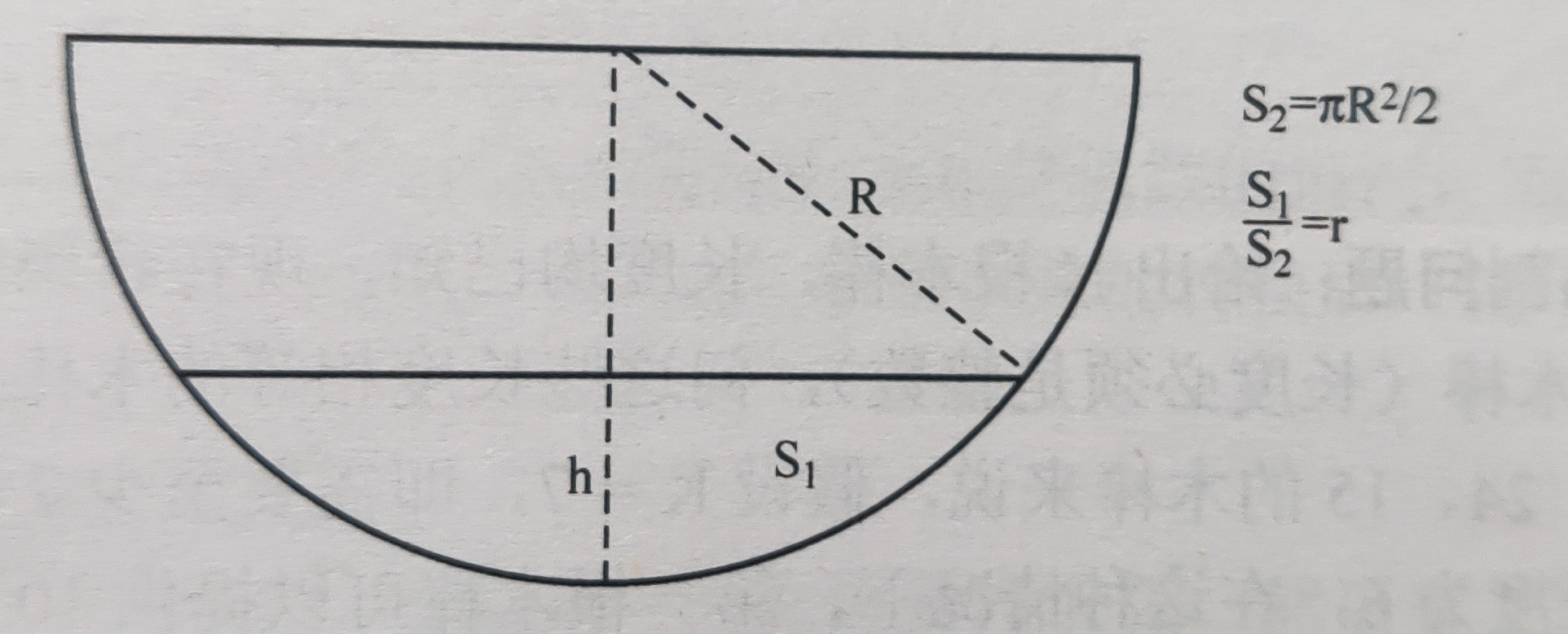
显然，随着 h 的升高，比例 r 一定增加，降低则一定减少。因此可以采用二分法。

解题代码：

const double PI = acos(-1.0);
const double eqs = 1e-5;
double fun(double R, double h){
	double alpha = 2 * acos((R - h) / R);
	double L = 2 * sqet(R * R - (R - h) * (R - h));
	double S1 = alpha * R * R / 2 - L * (R - h) / 2;
	double S2 = PI * R * R / 2;
	return S1 / S2;
}
double solve(double R, double r){
	double left, right, mid;
	left = 0;
	right = R;
	while (right - left > eqs){
		mid = (left + right) / 2;
		if(fun(R, mid) > r)    right - mid;
		else    left = mid;
	}
	return mid;
}

5.木棒切割问题

一个显而易见的结论：要求的木棒长度越长，则木棒的数量一定越小。

这个问题可以阶乘求解最后一个满足条件 “k >= K” 的长度 L ，不妨将其转化为求解第一个满足条件 “k < K” 的长度 L ，然后减一即可。

利用二分法的思想，求无法满足要求的最小长度，此长度减一便可以得到满足要求的最大长度。

#include <stdio.h>
#include <stdlib.h>

int Max(int arr[], int N);  //求数组的最大值
int f(int arr[], int L, int N);  //计算可以切出几个木棒的函数
int solve(int K, int arr[], int N);  //二分法查找满足条件的最大长度(通过不满足条件的最小长度-1间接求得)

int main(){
    int i;
    int N, K, num;
    printf("请问原本有几个木棒：");
    scanf("%d", &N);
    int *arr = (int*) calloc(sizeof(int), N);
    printf("请依次输入这些木棒:\n");
    for (i = 0; i < N; i++)    scanf("%d", &arr[i]);
    printf("请问要拆成几个木棒:");
    scanf("%d", &K);
    num = solve(K,arr, N);
    printf("%d", num);
    return 0;
}

int Max(int arr[], int N){
    int max = 0;
    for(int i = 0; i < N; i++)
        if(arr[i] > max)    max = arr[i];
    return max;
}

int f(int arr[], int L, int N){  //计算切割后小木棒总数
    int i;
    int sum=0; //切成sum个小木棒
    for (i = 0; i < N; i++)    sum += arr[i] / L;  //依次计算从每一根木棒中可以切出几个小木棒，累加
    return sum;
}

//长度与数量是负相关，长度越长，数量越少。
//此函数的目的是：找出使 k<K 的最小长度，将其减一便成为满足 k>=K 的最大长度。
int solve(int K, int arr[], int N){
    int left, right, mid;
    left = 0;
    right = Max(arr, N);
    while (left < right){
        mid = (left + right) / 2;
        if (f(arr, mid, N) < K)    right = mid;  //如果拆出的木棒不够多，则需要往长度更小的区间尝试
        else    left = mid + 1;  //如果数量足够，则需要往长度更大的区间尝试，并抛弃mid值（因为它并不符合k<K）
    }
    return right-1; //返回长度
}

三、快速幂

1.简单问题

先来看一个问题：给定三个正整数 a, b, m (a < 10⁹ , b < 10⁶ , 1 < m < 10⁹ )，求 a^b%m 。

可以用一段简单的代码解决，时间复杂度是 o(b) ：

long long fun(long long a, long long b, long long m){
	int i;
	long long num = 1;
	for (i = 0; i < b; i++)    num = num * a % m;
	return num;
}

为什么可以每一步都对 m 取模呢？

因为最终结果需要对 m 取模，而如果中间值大于 m ，它继续运算相当于 n * m + 余数 参与运算，n * m 部分注定会被除掉。

例如：
1
(m + 1) * n % m = n
而
1
2
(m + 1) % m = 1
1 * n % m = n
结果完全相同。

2.复杂问题

给定三个正整数 a, b, m (a < 10⁹ , b < 10¹⁸ , 1 < m < 10⁹ )，求 a^b%m 。

对于这个问题，显然按照之前的做法是不合适的，因为 o(n) 的复杂度在 10¹⁸ 面前也非常吃力，此时便可以使用快速幂的方法。

3.递归快速幂

快速幂基于以下事实：

如果 b 是奇数，那么有 a^b = a * a^b-1
如果 b 是偶数，那么有 a^b = a^{b / 2} * a^{b / 2}

显然，将 b 转换为偶数，向下拆分，持续递归，便可以更快地计算出幂。

解题代码：

long long fun(long long a, long long b, long long m){
	if (b == 0)    return 0;
	else if (b % 2 == 1)    return a * fun(a, b - 1, m) % m;
	else{
		long long temp = fun(a, b / 2, m);
		return temp * temp % m;
	}
}

当 b 为偶数时，应该先计算出 fun(a, b / 2, m) ，在用两个运算结果相乘，否则会递归运算两次。

4.迭代快速幂

若将 b 转化为二进制，便可以将 b 转换为若干二次幂之和。

例如：

13 的二进制是 1101 ，可得 13 = 2³ + 2² + 0 + 2⁰ = 8 + 4 + 0 + 1，a¹³ = a^{8 + 4 + 1} = a⁸ * a⁴ * a⁰ * a¹

又二进制仅有 0 和 1 ，可以用奇偶判断，因此可以无需转化。判断 b 的奇偶，如果为偶，说明此位上为 0 ，结果乘以 a⁰ 结果不变，无需运算；如果为奇，说明此为上为 1 ，结果应该乘以 a²ⁱ 。

解题思路：

初始化 num = 1 ，用于存放结果
判断 b 的奇偶性，如果为奇，则 num 乘以 a
将 a 平方，将 b 除以 2 (移除末位)

解题代码：

long long fun(long long a, long long b, long long m){
	long long num = 1;
	while (b > 0){
		if (b % 2 != 0)    num = num * a % m;
		a = a * a % m;
		b /= 2;
	}
	return num;
}

参考

算法笔记

基础算法笔记

SQL 系统结构上一篇

算法笔记贪心下一篇

算法笔记 二分法

一、二分查找

1.猜数字

2.线性查找

3.二分查找

3.查询元素区间

(1) 分析：

(2) 求 L ：

(3) 求 R：

4.解题模板

二、二分法扩展

1.根号

2.求根问题

3.一些错误

4.装水问题

5.木棒切割问题

三、快速幂

1.简单问题

2.复杂问题

3.递归快速幂

4.迭代快速幂

参考